Casos de Estudio
Análisis de Datos cinéticos
Descubriendo la Magia en la Reacción: Una Introducción a la Cinética Química
Introducción:
Bienvenidos a un fascinante viaje hacia el corazón de las reacciones químicas, donde la velocidad y el misterio se entrelazan. Como apasionado experto en química y amante del aprendizaje, hoy desentrañaremos el mundo de la cinética química. ¿Qué sucede realmente en esos matraces y tubos de ensayo cuando las sustancias reaccionan? ¡Acompáñenme mientras exploramos esta ciencia intrigante!
¿Qué es la Cinética Química?
La cinética química es la rama de la química que se sumerge en el estudio de las velocidades de las reacciones químicas y los factores que las afectan. Imaginen una coreografía molecular donde cada paso, cada giro y cada interacción contribuyen al fascinante ballet de la transformación química. Desde la combinación de sustancias hasta la formación de nuevos productos, la cinética química nos brinda las herramientas para comprender y controlar estos procesos.
Principales Conceptos:
- Velocidad de Reacción: La velocidad de reacción es la medida de qué tan rápido se están transformando los reactivos en productos. Es como capturar el instante preciso en el que la magia química cobra vida.
- Factores que Afectan la Velocidad:
Concentración de Reactivos: Cuanto más concentrados estén los reactivos, más colisiones tendrán y, por ende, más rápido ocurrirá la reacción.
Temperatura: El aumento de la temperatura energiza las moléculas, aumentando la probabilidad de colisiones exitosas.
Superficie de Contacto: En reacciones entre sólidos, una mayor superficie de contacto acelera la velocidad. - Leyes de la Cinética Química: La expresión matemática de la velocidad de reacción en función de la concentración de los reactivos nos lleva a las leyes de la cinética, como la ley de velocidad de primer y segundo orden.
Relevancia en el Mundo Real:
El entender cómo se desarrolla una reacción nos permite predecir su velocidad y los resultados. Esto es crucial en la síntesis de nuevos materiales, medicamentos y procesos industriales eficientes.
En el mundo de Excel y quimiometría, la cinética química también se conecta con la recopilación y análisis de datos experimentales. Graficar curvas de reacción y aplicar técnicas quimiométricas permite obtener información valiosa sobre la velocidad y los mecanismos de las reacciones.
Técnicas experimentales
Existen diversas técnicas experimentales para medir la velocidad de una reacción química. La elección de la técnica depende de la naturaleza de la reacción y de los componentes involucrados. Aquí te presento algunas de las técnicas más comunes:
- Método de Medición de la Variación de la Concentración:
Espectroscopía UV-Visible: Se mide la absorbancia de la luz a diferentes longitudes de onda a lo largo del tiempo. La variación en la absorbancia está relacionada con cambios en la concentración de reactivos y productos.
Cromatografía: Se monitorea la separación de componentes a medida que la reacción progresa. La velocidad se determina midiendo la altura o el área de los picos cromatográficos. - Método de Medición de Gases:
Desplazamiento de Gases: La liberación de gases, como el dióxido de carbono, se mide para determinar la velocidad de la reacción. Esto es común en reacciones que generan o consumen gases. - Método de Conductimetría:
Conductimetría: Se mide la conductividad eléctrica de la solución a medida que la reacción progresa. Cambios en la conductividad están relacionados con cambios en la concentración de iones. - Método de Pesada:
Pesada Continua: Se pesa el sistema reaccionante a intervalos regulares. La pérdida o ganancia de masa está relacionada con la velocidad de la reacción. - Método de Calorimetría:
Calorimetría: Se mide el calor liberado o absorbido durante la reacción. Cambios en la temperatura están directamente relacionados con la velocidad de la reacción. - Método de Seguimiento Visual:
Seguimiento Visual: En algunas reacciones, especialmente aquellas que involucran cambios de color, la velocidad puede medirse visualmente. Se observa y registra cómo cambian las características visuales de la mezcla reaccionante. - Método de Electroquímica:
- Electroquímica: Se mide la corriente eléctrica generada por la reacción redox. La velocidad se relaciona con la corriente medida.
Estas técnicas ofrecen diversas perspectivas para evaluar la velocidad de una reacción química. En muchos casos, se utilizan combinaciones de estas técnicas para obtener datos más precisos y comprensivos. Es importante considerar las condiciones experimentales y las limitaciones inherentes a cada método al seleccionar la técnica más apropiada.
Reacción de Primer Orden
Reacción Cinética de Primer Orden:
En una reacción cinética de primer orden, la velocidad de la reacción depende de la concentración de un solo reactivo elevado a la primera potencia. La ecuación matemática general para una reacción de primer orden es:
A \xrightarrow{k} \text{Productos} Donde:
- ( A ) es el reactivo.
- ( k ) es la constante de velocidad de primer orden.
La ecuación de la velocidad de reacción ((v)) para una reacción de primer orden se expresa como:
v = k[A]
Donde:
- ( [A] ) es la concentración del reactivo
La ecuación cinética de primer orden integrada describe cómo la concentración de un reactivo varía con el tiempo en una reacción de primer orden. La forma integrada de la ecuación diferencial de primer orden es:
[ \ln([A]_t) = -kt + \ln([A]_0) ]
Donde:
- ( [A]_t ) es la concentración del reactivo en el tiempo ( t ).
- ( [A]_0 ) es la concentración inicial del reactivo.
- ( k ) es la constante de velocidad de primer orden.
- ( \ln ) es la función logaritmo natural.
Esta ecuación muestra la relación lineal entre el logaritmo natural de la concentración del reactivo en un momento dado y el tiempo de reacción. Puedes utilizar esta ecuación para calcular la concentración en cualquier momento ( t ) si conoces la concentración inicial ( [A]_0 ), la constante de velocidad ( k ) y el tiempo ( t ).
Si necesitas calcular ( [A]_t ) directamente, puedes despejar ( [A]_t ) en términos de las otras variables:
[A]_t = [A]_0 \cdot e^{-kt} Esta fórmula expresa la concentración del reactivo en cualquier punto dado en función de la concentración inicial y la constante de velocidad.
Ejemplo en Python:
Vamos a simular una reacción de primer orden utilizando Python. Supongamos que tenemos una reacción de descomposición de un compuesto A, y queremos modelar la disminución de la concentración de A con el tiempo. Usaremos la ecuación de primer orden para ello.
import numpy as np
import matplotlib.pyplot as plt
# Definir la constante de velocidad de primer orden (k)
k = 0.05 # Ejemplo, ajusta según tu necesidad
# Definir la concentración inicial de A y el tiempo inicial y final
A0 = 1.0 # Concentración inicial
t0 = 0 # Tiempo inicial
tf = 20 # Tiempo final
# Crear un array de tiempo
t = np.linspace(t0, tf, 100)
# Calcular la concentración de A en función del tiempo para una reacción de primer orden
A = A0 * np.exp(-k * t)
# Graficar los resultados
plt.figure(figsize=(8, 5))
plt.plot(t, A, label='Concentración de A')
plt.title('Reacción de Primer Orden')
plt.xlabel('Tiempo')
plt.ylabel('Concentración de A')
plt.legend()
plt.show()Este código utiliza la biblioteca NumPy para realizar cálculos y Matplotlib para graficar. Puedes ajustar la constante de velocidad (k) y observar cómo cambia la velocidad de la reacción de primer orden a lo largo del tiempo. La gráfica resultante mostrará la disminución exponencial de la concentración de (A) con respecto al tiempo.
Reacción de Segundo Orden
En una reacción cinética de segundo orden, la velocidad de la reacción depende de la concentración de dos reactantes, y la ecuación general de una reacción de segundo orden es:
[ aA + bB \xrightarrow{k} \text{Productos} ]
donde ( a ) y ( b ) son los coeficientes estequiométricos de los reactantes ( A ) y ( B ), respectivamente, y ( k ) es la constante de velocidad de segundo orden.
Ecuación de Velocidad:
La ecuación de velocidad para una reacción de segundo orden es:
[ v = k[A][B] ]
donde ( [A] ) y ( [B] ) son las concentraciones de los reactantes ( A ) y ( B ), respectivamente.
Existen tres casos comunes para las reacciones de segundo orden, dependiendo de las condiciones iniciales y cómo varían las concentraciones:
- Reacción de Segundo Orden con Dos Moles Iniciales del Mismo Reactante: [ aA + aA \xrightarrow{k} \text{Productos} ] La ecuación de velocidad es: [ v = k[A]^2 ] La forma integrada de esta ecuación se obtiene resolviendo la ecuación diferencial correspondiente y depende de la concentración inicial de ( A ). La ecuación general es: [ \frac{1}{[A]_t} = \frac{1}{[A]_0} + kt ] donde ( [A]_t ) es la concentración de ( A ) en el tiempo ( t ), y ( [A]_0 ) es la concentración inicial de ( A ).
- Reacción de Segundo Orden con Dos Reactantes Distintos Iniciales: [ aA + bB \xrightarrow{k} \text{Productos} ] La ecuación de velocidad es: [ v = k[A][B] ] La forma integrada de esta ecuación depende de las concentraciones iniciales de ( A ) y ( B ). La ecuación general es: [ \frac{1}{[A]_t} = \frac{1}{[A]_0} + \frac{k}{[B]_0}t ] o [ \frac{1}{[B]_t} = \frac{1}{[B]_0} + \frac{k}{[A]_0}t ]
- Reacción de Segundo Orden con Exceso de uno de los Reactantes (Cinética de pseudo-primer orden): [ aA + bB \xrightarrow{k} \text{Productos} ] Supongamos que hay un exceso de ( B ), entonces ( [B]_0 ) se mantiene constante y ( [A]_0 ) varía. La ecuación de velocidad se convierte en: [ v = k[A] ] La forma integrada de esta ecuación es: [ [A]_t = \frac{1}{kt} ]
Estas son las ecuaciones generales para una reacción de segundo orden bajo diferentes condiciones iniciales y restricciones. La resolución de la ecuación diferencial asociada proporciona estas formas integradas. En cada caso, la interpretación y aplicación de las ecuaciones pueden variar según el contexto específico de la reacción.
Vamos a simular una reacción de segundo orden utilizando Python. Supongamos que tenemos una reacción entre dos reactantes ( A ) y ( B ) que produce productos, y queremos modelar la variación de las concentraciones con el tiempo.
La ecuación de velocidad para una reacción de segundo orden es:
[ v = k[A][B] ]
Vamos a utilizar la biblioteca NumPy y Matplotlib para calcular y visualizar las concentraciones de ( A ) y ( B ) a lo largo del tiempo. En este ejemplo, asumiremos una concentración inicial de ( A ) y ( B ) y una constante de velocidad ( k ).
import numpy as np
import matplotlib.pyplot as plt
# Definir la constante de velocidad de segundo orden (k)
k = 0.02 # Ejemplo, ajusta según tu necesidad
# Definir las concentraciones iniciales de A y B y el tiempo inicial y final
A0 = 1.0 # Concentración inicial de A
B0 = 0.5 # Concentración inicial de B
t0 = 0 # Tiempo inicial
tf = 50 # Tiempo final
# Crear un array de tiempo
t = np.linspace(t0, tf, 100)
# Calcular las concentraciones de A y B en función del tiempo para una reacción de segundo orden
A = A0 / (1 + k * B0 * t)
B = B0 / (1 + k * A0 * t)
# Graficar los resultados
plt.figure(figsize=(8, 5))
plt.plot(t, A, label='Concentración de A')
plt.plot(t, B, label='Concentración de B')
plt.title('Reacción de Segundo Orden')
plt.xlabel('Tiempo')
plt.ylabel('Concentración')
plt.legend()
plt.show()Este código modela las concentraciones de ( A ) y ( B ) en función del tiempo para una reacción de segundo orden. Puedes ajustar la constante de velocidad ( k ), las concentraciones iniciales y el tiempo final para explorar cómo cambian las concentraciones durante la reacción.
Reacciones Consecutivas
Las reacciones consecutivas son un tipo de secuencia de reacciones en la que el producto de una reacción se convierte en el reactante de otra reacción. Este proceso puede ocurrir varias veces, creando una cadena de reacciones consecutivas. En estas reacciones, los productos de una etapa se convierten en los reactantes de la siguiente, y así sucesivamente.
El ejemplo más simple de una reacción consecutiva es cuando una especie (A) se convierte en otra especie (B) en una primera etapa, y luego (B) se convierte en (C) en una segunda etapa. La secuencia se puede representar como:
[ A \xrightarrow{k_1} B \xrightarrow{k_2} C ]
Donde (k_1) y (k_2) son las constantes de velocidad de la primera y segunda etapa, respectivamente.
Vamos a simular una reacción consecutiva en Python utilizando las ecuaciones diferenciales y NumPy. En este ejemplo, consideraremos las siguientes ecuaciones cinéticas:
[ \frac{d[A]}{dt} = -k_1[A] ]
[ \frac{d[B]}{dt} = k_1[A] – k_2[B] ]
[ \frac{d[C]}{dt} = k_2[B] ]
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Definir las ecuaciones diferenciales para la reacción consecutiva
def reaction_system(y, t, k1, k2):
A, B, C = y
dAdt = -k1 * A
dBdt = k1 * A - k2 * B
dCdt = k2 * B
return [dAdt, dBdt, dCdt]
# Condiciones iniciales y constantes de velocidad
initial_conditions = [1.0, 0.0, 0.0] # [A0, B0, C0]
k1 = 0.1
k2 = 0.05
# Crear un array de tiempo
t = np.linspace(0, 50, 100)
# Resolver las ecuaciones diferenciales utilizando odeint
solution = odeint(reaction_system, initial_conditions, t, args=(k1, k2))
# Graficar los resultados
plt.figure(figsize=(8, 5))
plt.plot(t, solution[:, 0], label='A')
plt.plot(t, solution[:, 1], label='B')
plt.plot(t, solution[:, 2], label='C')
plt.title('Reacción Consecutiva')
plt.xlabel('Tiempo')
plt.ylabel('Concentración')
plt.legend()
plt.show()Este código utiliza el método odeint de SciPy para resolver las ecuaciones diferenciales asociadas con la reacción consecutiva. Puedes ajustar las condiciones iniciales y las constantes de velocidad para explorar diferentes escenarios de reacciones consecutivas.
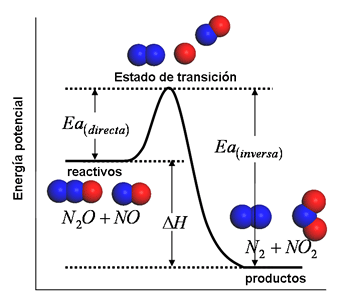
Reacciones Reversibles
Las reacciones reversibles son procesos químicos en los que los reactantes se convierten en productos, y al mismo tiempo, los productos pueden revertirse para formar nuevamente los reactantes. Este fenómeno se representa mediante una doble flecha ((\rightleftharpoons)) que indica la reversibilidad de la reacción. La ecuación general de una reacción reversible se expresa como:
[ aA + bB \rightleftharpoons cC + dD ]
Donde ( a, b, c, ) y ( d ) son los coeficientes estequiométricos de los reactantes y productos. La velocidad de la reacción directa está influenciada por la concentración de los reactantes, mientras que la velocidad de la reacción inversa depende de la concentración de los productos.
Matemática de las Reacciones Reversibles:
La expresión matemática que describe la velocidad de una reacción reversible sigue la ley de acción de masas, y para una reacción general ( aA + bB \rightleftharpoons cC + dD ), la expresión de la velocidad se puede escribir como:
[ v = k_f [A]^a [B]^b – k_r [C]^c [D]^d ]
Donde:
- ( v ) es la velocidad neta de la reacción.
- ( k_f ) y ( k_r ) son las constantes de velocidad para la reacción directa e inversa, respectivamente.
- ( [A], [B], [C], ) y ( [D] ) son las concentraciones de los respectivos reactantes y productos.
La ecuación de velocidad refleja que la velocidad neta ((v)) es la diferencia entre la velocidad de la reacción directa ((k_f [A]^a [B]^b)) y la velocidad de la reacción inversa ((k_r [C]^c [D]^d)). La forma exacta de esta ecuación dependerá de la estequiometría específica de la reacción reversible.
Ejemplo en Python:
Vamos a simular una reacción reversible utilizando Python. Supongamos que tenemos la reacción (A + B \rightleftharpoons C), y queremos modelar cómo cambian las concentraciones de los reactantes y productos con el tiempo.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Definir las ecuaciones diferenciales para la reacción reversible
def reaction_system(y, t, kf, kr):
A, B, C = y
dAdt = -kf * A * B + kr * C
dBdt = -kf * A * B + kr * C
dCdt = kf * A * B - kr * C
return [dAdt, dBdt, dCdt]
# Condiciones iniciales y constantes de velocidad
initial_conditions = [1.0, 2.0, 0.0] # [A0, B0, C0]
kf = 0.1
kr = 0.05
# Crear un array de tiempo
t = np.linspace(0, 50, 100)
# Resolver las ecuaciones diferenciales utilizando odeint
solution = odeint(reaction_system, initial_conditions, t, args=(kf, kr))
# Graficar los resultados
plt.figure(figsize=(8, 5))
plt.plot(t, solution[:, 0], label='A')
plt.plot(t, solution[:, 1], label='B')
plt.plot(t, solution[:, 2], label='C')
plt.title('Reacción Reversible')
plt.xlabel('Tiempo')
plt.ylabel('Concentración')
plt.legend()
plt.show()Este código utiliza el método odeint de SciPy para resolver las ecuaciones diferenciales asociadas con la reacción reversible. Puedes ajustar las condiciones iniciales y las constantes de velocidad para explorar diferentes escenarios de reacciones reversibles.
Reacciones Cinéticas por Integración Numérica
La simulación cinética por integración numérica es un enfoque computacional utilizado para modelar y estudiar el comportamiento temporal de sistemas químicos o biológicos. Esta técnica se basa en la resolución numérica de las ecuaciones diferenciales que describen las tasas de cambio de las concentraciones de diferentes especies químicas a lo largo del tiempo.
En el contexto de la cinética química, las ecuaciones diferenciales describen cómo cambian las concentraciones de los reactantes y productos en función del tiempo. Estas ecuaciones suelen derivarse a partir de mecanismos detallados de reacción y la ley de acción de masas. La resolución numérica de estas ecuaciones proporciona una representación detallada de la evolución temporal del sistema.
El método más común para realizar la integración numérica en cinética química es el método de Euler o métodos más avanzados como el método de Runge-Kutta. Estos métodos dividen el tiempo en pequeños incrementos y calculan las concentraciones en cada paso temporal, utilizando las tasas de cambio proporcionadas por las ecuaciones diferenciales.
Pasos generales para la simulación cinética por integración numérica:
- Definición de Ecuaciones Diferenciales: Establecer las ecuaciones diferenciales que describen las tasas de cambio de las concentraciones de las especies químicas en función del tiempo.
- Elección de Método Numérico: Seleccionar un método numérico adecuado para la integración, como el método de Euler o métodos más precisos como el método de Runge-Kutta.
- Definición de Condiciones Iniciales: Especificar las condiciones iniciales del sistema, es decir, las concentraciones iniciales de las especies químicas.
- División del Tiempo: Dividir el tiempo en pequeños incrementos.
- Iteración Numérica: Iterar a través del tiempo, calculando las concentraciones en cada paso utilizando el método numérico elegido.
- Almacenamiento de Resultados: Almacenar los resultados de las simulaciones, como las concentraciones de las especies químicas a lo largo del tiempo.
- Análisis de Resultados: Analizar y visualizar los resultados para obtener información sobre la dinámica temporal del sistema.
Este enfoque de simulación es valioso para comprender la cinética de las reacciones químicas, prever el comportamiento de los sistemas y explorar cómo diferentes condiciones afectan las trayectorias temporales de las concentraciones. Además, la simulación numérica es particularmente útil cuando los sistemas son complejos y no se pueden resolver de manera analítica.
Para proporcionar un ejemplo de simulación cinética por integración numérica utilizando el método de Runge-Kutta, consideremos la reacción de primer orden:
[ A \xrightarrow{k} B ]
donde ( A ) es el reactante, ( B ) es el producto, y ( k ) es la constante de velocidad de primer orden. La ecuación diferencial asociada es:
[ \frac{d[A]}{dt} = -k[A] ]
Vamos a simular esta reacción utilizando Python y el método de Runge-Kutta de cuarto orden. Utilizaremos el paquete scipy que proporciona la función odeint para integración numérica. Asegúrate de tener scipy instalado antes de ejecutar el código:
pip install scipyAquí está el código:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Definir la ecuación diferencial para la reacción de primer orden
def reaction_equation(A, t, k):
dAdt = -k * A
return dAdt
# Parámetros de la simulación
k = 0.1 # constante de velocidad de primer orden
A0 = 1.0 # concentración inicial de A
t = np.linspace(0, 10, 100) # array de tiempo
# Resolver la ecuación diferencial utilizando el método de Runge-Kutta de cuarto orden
solution = odeint(reaction_equation, A0, t, args=(k,))
# Graficar los resultados
plt.plot(t, solution, label='A')
plt.title('Simulación de la Reacción de Primer Orden')
plt.xlabel('Tiempo')
plt.ylabel('Concentración de A')
plt.legend()
plt.show()Este código utiliza el método de Runge-Kutta de cuarto orden para resolver la ecuación diferencial asociada a la reacción de primer orden. La función odeint realiza la integración numérica y produce una solución para la concentración de ( A ) en función del tiempo.
Puedes ajustar los parámetros como la constante de velocidad ( k ), la concentración inicial de ( A ), y el tiempo de simulación para explorar cómo afectan estos factores la dinámica de la reacción. Este enfoque es escalable a sistemas más complejos y reacciones de orden superior.
Usando em método Runge-Kutta para ecuaciones de Segundo Orden
El método de Runge-Kutta de cuarto orden es un método numérico ampliamente utilizado para resolver ecuaciones diferenciales ordinarias (EDO). Para entender las matemáticas detrás del método, consideremos un sistema de EDOs general:
[ \frac{dy}{dt} = f(t, y) ]
donde ( y ) es el vector de variables de estado y ( f(t, y) ) es la función que describe la tasa de cambio de ( y ) en función del tiempo ( t ).
El método de Runge-Kutta de cuarto orden actualiza las variables de estado ( y ) en pequeños pasos de tiempo, utilizando la siguiente fórmula iterativa:
[ y_{n+1} = y_n + \frac{1}{6} (k_1 + 2k_2 + 2k_3 + k_4) ]
donde:
- ( y_n ) es el valor actual de las variables de estado en el paso ( n ).
- ( h ) es el tamaño del paso de tiempo.
- ( k_1 ), ( k_2 ), ( k_3 ), y ( k_4 ) son aproximaciones de la tasa de cambio calculadas en diferentes puntos a lo largo del intervalo de tiempo ( [t_n, t_{n+1}] ): [ k_1 = h \cdot f(t_n, y_n) ]
[ k_2 = h \cdot f(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}) ]
[ k_3 = h \cdot f(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}) ]
[ k_4 = h \cdot f(t_n + h, y_n + k_3) ]
Estas aproximaciones se calculan en diferentes puntos a lo largo del intervalo de tiempo, y la combinación ponderada de estas aproximaciones se utiliza para actualizar las variables de estado.
Aplicando este método al sistema de EDOs asociado a la reacción de segundo orden ( A + B \rightarrow C ), las ecuaciones diferenciales son:
[ \frac{dA}{dt} = -k \cdot A \cdot B ]
[ \frac{dB}{dt} = -k \cdot A \cdot B ]
[ \frac{dC}{dt} = k \cdot A \cdot B ]
Estas ecuaciones se pueden implementar en el método de Runge-Kutta de cuarto orden para simular la cinética de la reacción de segundo orden.
Vamos a simular una reacción de segundo orden utilizando el método de Runge-Kutta de cuarto orden. Consideraremos la siguiente reacción:
[ A + B \xrightarrow{k} C ]
donde ( A ) y ( B ) son reactantes, ( C ) es el producto, y ( k ) es la constante de velocidad de segundo orden. Las ecuaciones diferenciales asociadas son:
[ \frac{d[A]}{dt} = -k[A][B] ]
[ \frac{d[B]}{dt} = -k[A][B] ]
[ \frac{d[C]}{dt} = k[A][B] ]
Aquí está el código en Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Definir las ecuaciones diferenciales para la reacción de segundo orden
def reaction_equations(y, t, k):
A, B, C = y
dAdt = -k * A * B
dBdt = -k * A * B
dCdt = k * A * B
return [dAdt, dBdt, dCdt]
# Parámetros de la simulación
k = 0.02 # constante de velocidad de segundo orden
A0 = 1.0 # concentración inicial de A
B0 = 0.5 # concentración inicial de B
C0 = 0.0 # concentración inicial de C
initial_conditions = [A0, B0, C0]
t = np.linspace(0, 50, 100) # array de tiempo
# Resolver las ecuaciones diferenciales utilizando el método de Runge-Kutta de cuarto orden
solution = odeint(reaction_equations, initial_conditions, t, args=(k,))
# Graficar los resultados
plt.plot(t, solution[:, 0], label='A')
plt.plot(t, solution[:, 1], label='B')
plt.plot(t, solution[:, 2], label='C')
plt.title('Simulación de la Reacción de Segundo Orden')
plt.xlabel('Tiempo')
plt.ylabel('Concentración')
plt.legend()
plt.show()Este código utiliza el método de Runge-Kutta de cuarto orden para resolver las ecuaciones diferenciales asociadas a la reacción de segundo orden. Puedes ajustar los parámetros como la constante de velocidad ( k ), las concentraciones iniciales de ( A ), ( B ) y ( C ), y el tiempo de simulación para explorar cómo afectan estos factores la dinámica de la reacción. Este enfoque también se puede adaptar para reacciones de segundo orden más complejas.
Deconvolución de espectros
La deconvolución de espectros es una técnica analítica utilizada en espectroscopía para separar o descomponer un espectro complejo en sus componentes individuales, especialmente cuando hay superposición de señales. Esta técnica es ampliamente aplicada en diversas áreas como la espectroscopía de resonancia magnética nuclear (RMN), espectroscopía de infrarrojo (IR), espectroscopía de masas y otras técnicas espectroscópicas.
Principio Básico:
En un espectro complejo, las señales de diferentes especies químicas pueden superponerse, lo que dificulta la identificación y cuantificación de cada componente. La deconvolución busca resolver este problema descomponiendo el espectro en sus componentes individuales, conocidos como picos o bandas.
Proceso de Deconvolución:
- Selección del Método:
Se elige un método de deconvolución adecuado según la naturaleza del espectro y la información disponible.
Algunos métodos comunes incluyen el método de mínimos cuadrados, métodos basados en funciones de forma (como funciones de Lorentz o Gaussianas), y métodos de descomposición espectral. - Modelado de Perfiles de Pico:
Se selecciona un modelo matemático que describa los perfiles de los picos en el espectro. Los perfiles pueden ser gaussianos, lorentzianos u otros, dependiendo de la forma de las bandas en el espectro. - Ajuste de Parámetros:
Se ajustan los parámetros del modelo, como la posición del pico, la altura y el ancho, para que el modelo se ajuste mejor al espectro original.
La optimización de estos parámetros se realiza típicamente mediante algoritmos numéricos que minimizan la diferencia entre el modelo y el espectro real. - Aplicación del Modelo:
Se aplica el modelo ajustado al espectro completo para identificar y cuantificar las contribuciones de cada componente. - Validación y Ajustes Adicionales:
Se valida el resultado de la deconvolución y se realizan ajustes adicionales si es necesario para mejorar la calidad del ajuste.
Aplicaciones:
- Espectroscopía de Resonancia Magnética Nuclear (RMN):
En la RMN, la deconvolución es útil para separar las señales superpuestas de diferentes núcleos atómicos en una molécula. - Espectroscopía de Infrarrojo (IR):
Permite la separación de bandas de vibración superpuestas, facilitando la identificación de grupos funcionales en moléculas. - Espectrometría de Masas:
Ayuda en la identificación de picos de masas individuales en un espectro de masas complejo. - Espectroscopía Óptica:
Utilizada para descomponer espectros de absorción, emisión o dispersión en componentes individuales.
Desafíos y Consideraciones:
- La deconvolución puede ser desafiante, especialmente cuando hay ruido en el espectro.
- La elección del modelo y los parámetros iniciales afecta la calidad del resultado de la deconvolución.
- Es importante considerar la resolución del espectrómetro y la calidad de los datos experimentales.
En resumen, la deconvolución de espectros es una herramienta poderosa para extraer información detallada de espectros complejos, permitiendo una mejor comprensión y caracterización de las muestras analizadas en diversas áreas científicas.
Matemáticas detrás de la Deconvolución
La matemática detrás de la deconvolución de espectros implica la descripción matemática de los perfiles de los picos que se encuentran en el espectro. Comúnmente, se utilizan funciones de forma, como Gaussianas o Lorentzianas, para modelar estos perfiles. La deconvolución busca ajustar estos perfiles a las señales superpuestas en el espectro, y los parámetros clave que se ajustan son la posición, la intensidad y la anchura de los picos.
Vamos a explorar cómo se define matemáticamente un pico y cómo se ajustan estos parámetros:
1. Funciones de Perfil de Pico:
- Gaussiana:
La función de Gaussiana está dada por la fórmula: [ f(x) = A \cdot e^{-\frac{(x – \mu)^2}{2\sigma^2}} ] donde: - ( A ) es la altura del pico.
- ( \mu ) es la posición del pico (media).
- ( \sigma ) es la desviación estándar, que controla la anchura del pico.
- Lorentziana:
La función de Lorentziana está dada por la fórmula: [ f(x) = \frac{A}{1 + \left(\frac{x – \mu}{\frac{\gamma}{2}}\right)^2} ] donde: - ( A ) es la altura del pico.
- ( \mu ) es la posición del pico (centro).
- ( \gamma ) es la anchura a media altura, que controla la anchura del pico.
2. Ajuste de Parámetros:
El proceso de ajuste implica encontrar los valores óptimos de los parámetros ((A), (\mu), (\sigma) o (\gamma)) que minimizan la diferencia entre el modelo de pico y los datos experimentales. Este ajuste se realiza mediante técnicas de optimización numérica, como el método de mínimos cuadrados o algoritmos más avanzados.
3. Deconvolución del Espectro:
- Supongamos que tenemos un espectro con (N) picos superpuestos. La función total del espectro ((F(x))) es la suma de las funciones de perfil de cada pico: [ F(x) = \sum_{i=1}^{N} f_i(x) ]
- El objetivo es ajustar los parámetros ((A_i), (\mu_i), (\sigma_i) o (\gamma_i)) de cada función de perfil para que la suma se ajuste mejor al espectro experimental.
4. Algoritmo de Deconvolución:
- Inicialización: Establecer valores iniciales para los parámetros.
- Iteración: Utilizar un algoritmo de optimización para ajustar iterativamente los parámetros.
- Convergencia: Detener el proceso cuando los parámetros convergen a valores estables.
5. Resultados:
Los resultados finales de la deconvolución son los valores óptimos de los parámetros para cada pico. Estos parámetros proporcionan información sobre la posición, intensidad y anchura de cada componente en el espectro.
Es importante señalar que la deconvolución puede ser sensible a las condiciones iniciales y al ruido en el espectro, por lo que se requiere cuidado en la elección de modelos y en la calidad de los datos experimentales. Además, métodos más avanzados pueden considerar restricciones adicionales, como la positividad de las alturas de los picos o la relación entre las anchuras de los picos.
Deconvolución de espectros UV-Visible
En la deconvolución de espectros, los términos “anchura”, “intensidad” y “posición” se refieren a los parámetros de los picos que se están ajustando en el proceso de descomposición del espectro. Estos parámetros están asociados con las funciones de forma que modelan los picos individuales en el espectro.
- Posición (Centro) del Pico ((\mu)):
- La posición de un pico en un espectro se refiere al valor en el eje x donde se encuentra el pico. En el contexto de funciones de forma como las Gaussianas o Lorentzianas, (\mu) representa la posición del centro del pico. Un cambio en (\mu) desplaza el pico a lo largo del eje x.
- Intensidad del Pico (Altura o Amplitud) ((A)):
- La intensidad de un pico se refiere a la altura máxima del pico. En el contexto de funciones de forma, (A) representa la altura o amplitud del pico. Un cambio en (A) afecta la altura del pico en el espectro.
- Anchura del Pico ((\sigma) o (\gamma)):
- La anchura de un pico se refiere a qué tan ancho o estrecho es el pico en el espectro. En funciones de forma como Gaussianas, la anchura se describe mediante la desviación estándar ((\sigma)), mientras que en funciones de Lorentzianas se usa la anchura a media altura ((\gamma)). Cambiar (\sigma) o (\gamma) afecta la forma y el ancho del pico.
En el caso específico de la deconvolución de espectros UV-Visible, las funciones de forma utilizadas para modelar los picos pueden ser Gaussianas o Lorentzianas, dependiendo de la naturaleza de las bandas en el espectro. La elección entre estas funciones depende de la forma de las bandas y del comportamiento de absorción o emisión en la región UV-Visible.
Matemáticas de la Deconvolución en Espectroscopía UV-Visible:
- Modelado de Picos:
- Para una banda de absorción, por ejemplo, se puede utilizar una función de Lorentziana o Gaussiana para modelar el perfil del pico.
- En el caso de una Lorentziana: ( F(x) = \frac{A}{1 + \left(\frac{x – \mu}{\frac{\gamma}{2}}\right)^2} )
- En el caso de una Gaussiana: ( F(x) = A \cdot e^{-\frac{(x – \mu)^2}{2\sigma^2}} )
- Ajuste de Parámetros:
- Se busca ajustar los parámetros (A), (\mu), y (\gamma) o (\sigma) para cada pico de absorción en el espectro UV-Visible.
- Deconvolución:
- La deconvolución implica ajustar simultáneamente múltiples picos en el espectro para obtener sus posiciones, intensidades y anchuras.
- Optimización Numérica:
- Algoritmos de optimización numérica, como el método de mínimos cuadrados, se utilizan para encontrar los valores óptimos de los parámetros que minimizan la diferencia entre el modelo y el espectro real.
En resumen, la deconvolución en espectroscopía UV-Visible involucra el ajuste de funciones de forma a las bandas de absorción para extraer información sobre las posiciones, intensidades y anchuras de los picos que contribuyen al espectro.
Realizando una Deconvolución de espectros
Realizar una deconvolución de espectros implica varios pasos, desde la preparación de los datos hasta la aplicación de algoritmos de deconvolución. Aquí hay una guía general de los pasos necesarios:
Pasos para la Deconvolución de Espectros:
- Preparación de Datos:
- Obtén los datos espectroscópicos. Asegúrate de tener un conjunto de datos de buena calidad y con baja interferencia de ruido.
- Elección del Método de Deconvolución:
- Selecciona un método de deconvolución adecuado para tu tipo de espectro y los picos que estás intentando separar. Puedes optar por métodos basados en funciones de forma, como Gaussianas o Lorentzianas, o utilizar métodos avanzados basados en transformadas o algoritmos de optimización.
- Selección de Modelos de Picos:
- Elige funciones de forma que representen adecuadamente los picos en tu espectro. Pueden ser Gaussianas, Lorentzianas u otros perfiles según la forma de las bandas en tu espectro.
- Ajuste Inicial de Parámetros:
- Proporciona valores iniciales para los parámetros del modelo, como la posición, la intensidad y la anchura de los picos.
- Optimización de Parámetros:
- Aplica algoritmos de optimización numérica, como el método de mínimos cuadrados, para ajustar los parámetros del modelo y minimizar la diferencia entre el modelo y los datos experimentales.
- Convergencia y Validación:
- Verifica la convergencia del algoritmo y valida los resultados de la deconvolución. Puedes ajustar la configuración del algoritmo o realizar ajustes manuales si es necesario.
- Análisis de Resultados:
- Examina los resultados obtenidos, como las posiciones, intensidades y anchuras de los picos de cada componente en el espectro.
Ejemplo de Deconvolución con Python:
Supongamos que tienes un espectro UV-Visible con dos picos superpuestos y deseas realizar la deconvolución. Utilizaremos la biblioteca lmfit para ajustar funciones de Gaussiana a los picos.
import numpy as np
import matplotlib.pyplot as plt
from lmfit import Model
# Generar datos de ejemplo con dos picos superpuestos
x = np.linspace(200, 800, 400)
y = 50 * np.exp(-(x - 400)**2 / (2 * 30**2)) + 30 * np.exp(-(x - 600)**2 / (2 * 40**2)) + np.random.normal(0, 5, size=len(x))
# Definir modelo de Gaussiana
def gaussian(x, amp, cen, wid):
return amp * np.exp(-(x - cen)**2 / (2 * wid**2))
# Crear modelo para cada pico
model1 = Model(gaussian, prefix='p1_')
model2 = Model(gaussian, prefix='p2_')
# Unir modelos
model = model1 + model2
# Configurar parámetros iniciales
params = model.make_params(p1_amp=40, p1_cen=400, p1_wid=20, p2_amp=20, p2_cen=600, p2_wid=30)
# Ajustar modelo a los datos
result = model.fit(y, params, x=x)
# Visualizar resultados
result.plot_fit()
plt.title('Deconvolución de Espectro UV-Visible')
plt.xlabel('Longitud de Onda (nm)')
plt.ylabel('Intensidad')
plt.show()
# Imprimir parámetros ajustados
print(result.params)Este es un ejemplo simple donde generamos datos de dos picos Gaussianos superpuestos. Luego, utilizamos lmfit para ajustar dos funciones de Gaussiana al espectro y visualizamos los resultados. Este es solo un ejemplo básico, y la deconvolución en situaciones reales puede requerir ajustes adicionales y métodos más avanzados según la complejidad del espectro y la cantidad de picos.
Ecuación de Van der Waals
La ecuación de Van der Waals es una ecuación de estado modificada que describe el comportamiento de los gases reales, teniendo en cuenta las interacciones moleculares entre las partículas de gas. Fue propuesta por Johannes Diderik van der Waals en 1873 y es una mejora respecto a la ecuación de estado ideal, que asume condiciones ideales en las que las partículas de gas no interactúan entre sí.
La forma general de la ecuación de Van der Waals para un mol de gas es:
[ \left(P + a\left(\frac{n}{V}\right)^2\right)\left(V – nb\right) = nRT ]
donde:
- ( P ) es la presión.
- ( V ) es el volumen.
- ( n ) es la cantidad de sustancia (número de moles).
- ( R ) es la constante de los gases.
- ( T ) es la temperatura absoluta.
- ( a ) y ( b ) son parámetros empíricos que dependen de la sustancia.
Explicación Detallada:
- Correcciones para Presión (a):
- El término ( a\left(\frac{n}{V}\right)^2 ) corrige la presión, teniendo en cuenta las fuerzas atractivas entre las moléculas. ( a ) es una medida de la fuerza de atracción entre las partículas y se relaciona con la polaridad molecular.
- Correcciones para Volumen (nb):
- El término ( nb ) corrige el volumen ocupado por las moléculas, teniendo en cuenta que las moléculas no son puntos puntuales. ( b ) es una medida del volumen ocupado por una molécula.
- Ecuación Resultante:
- La ecuación completa es una modificación de la ley de los gases ideales (( PV = nRT )) que tiene en cuenta las interacciones moleculares. A bajas presiones y altas temperaturas, la ecuación de Van der Waals se reduce a la ley de los gases ideales.
- Diagrama de Van der Waals:
- En un diagrama de Van der Waals (presión vs. volumen), la ecuación representa una curva más realista para los gases reales en comparación con la línea recta de la ley de los gases ideales.
- Punto de Ebullición y Condensación:
- La ecuación de Van der Waals proporciona una explicación más precisa de los puntos de ebullición y condensación de las sustancias en comparación con la ley de los gases ideales.
- Limitaciones:
- Aunque la ecuación mejora la descripción del comportamiento de los gases reales, tiene sus limitaciones, especialmente a altas presiones y bajas temperaturas. Otras ecuaciones de estado más complejas, como la ecuación de estado de Redlich-Kwong o la ecuación de estado de Peng-Robinson, han sido desarrolladas para abordar estas limitaciones en contextos específicos.
En resumen, la ecuación de Van der Waals es una herramienta valiosa para describir el comportamiento de los gases reales al considerar las fuerzas moleculares y el volumen ocupado por las moléculas. Aunque ha sido superada en precisión por ecuaciones más avanzadas, sigue siendo fundamental para comprender la teoría de los gases reales y las interacciones moleculares en la termodinámica.
Usando Python
Puedes utilizar Python y la biblioteca Matplotlib para graficar la ecuación de Van der Waals variando la temperatura. Aquí hay un ejemplo básico de cómo podrías hacerlo:
import numpy as np
import matplotlib.pyplot as plt
# Definir la ecuación de Van der Waals
def van_der_waals(P, V, n, R, T, a, b):
return (P + a * (n / V)**2) * (V - n * b) - n * R * T
# Parámetros para el gas (ajusta según tu caso)
n = 1 # moles
R = 8.314 # J/(mol K), constante de los gases
a = 3.59 # parámetro 'a' en (L^2 atm)/(mol^2)
b = 0.0427 # parámetro 'b' en L/mol
# Rango de volúmenes y presiones
V_range = np.linspace(0.1, 5, 100)
T_values = [300, 400, 500] # diferentes temperaturas
# Graficar para diferentes temperaturas
plt.figure(figsize=(10, 6))
for T in T_values:
P_values = [van_der_waals(P, V, n, R, T, a, b) for V in V_range]
plt.plot(V_range, P_values, label=f'T = {T} K')
# Configuración del gráfico
plt.title('Ecuación de Van der Waals: Presión vs Volumen')
plt.xlabel('Volumen (L)')
plt.ylabel('Presión (atm)')
plt.legend()
plt.grid(True)
plt.show()En este ejemplo, he definido una función van_der_waals que toma la presión (P), el volumen (V), la cantidad de sustancia (n), la constante de los gases (R), la temperatura (T), y los parámetros empíricos a y b de la ecuación de Van der Waals. Luego, he graficado la ecuación para diferentes temperaturas.
Ajusta los valores de a, b, y otros parámetros según las características específicas de tu gas y experimento. Este es solo un ejemplo básico y puedes personalizarlo según tus necesidades.
Modelo Cazador Presa (Lotka-Volterra)
El modelo cazador-presa, también conocido como el modelo Lotka-Volterra, es un conjunto de ecuaciones diferenciales utilizado para describir las interacciones entre dos especies en un ecosistema: una especie depredadora (cazadora) y una especie presa. Este modelo fue propuesto de forma independiente por Alfred Lotka y Vito Volterra en la década de 1920, y ha sido fundamental en la ecología matemática para entender las dinámicas de población en sistemas biológicos.
Ecuaciones del Modelo Lotka-Volterra:
El modelo Lotka-Volterra consta de dos ecuaciones diferenciales acopladas, una para la especie presa ((x)) y otra para la especie depredadora ((y)):
- Para la especie presa ((x)):
[ \frac{dx}{dt} = \alpha x – \beta xy ] - Para la especie depredadora ((y)):
[ \frac{dy}{dt} = \delta xy – \gamma y ]
Donde:
- (x) y (y) son las poblaciones de presas y depredadores, respectivamente.
- (t) es el tiempo.
- (\alpha), (\beta), (\gamma), y (\delta) son parámetros que representan tasas de reproducción, tasas de depredación y competencia, y tasas de mortalidad, respectivamente.
Explicación Detallada:
- Especie Presa ((x)):
- (\frac{dx}{dt} = \alpha x) representa la tasa de crecimiento natural de la población de presas. (\alpha) es la tasa intrínseca de crecimiento de la especie presa en ausencia de depredadores.
- (-\beta xy) representa la tasa de disminución de la población de presas debido a la depredación. (\beta) controla la eficiencia de caza de los depredadores y (xy) representa la interacción entre presas y depredadores.
- Especie Depredadora ((y)):
- (\frac{dy}{dt} = \delta xy) representa la tasa de crecimiento de la población de depredadores debido a la captura de presas. (\delta) es la eficiencia de conversión de presas en nuevos depredadores.
- (-\gamma y) representa la tasa de disminución de la población de depredadores debido a la mortalidad natural. (\gamma) es la tasa intrínseca de mortalidad de la especie depredadora.
Comportamiento del Modelo:
- Ciclos de Población:
- El modelo Lotka-Volterra predice ciclos de población para ambas especies. Cuando la población de presas aumenta, más presas están disponibles para ser cazadas, lo que aumenta la población de depredadores. A medida que la población de depredadores aumenta, disminuye la población de presas, lo que a su vez reduce la población de depredadores.
- Estabilidad y Equilibrios:
- Los equilibrios del sistema representan estados en los que las tasas de crecimiento y disminución se equilibran. Estos equilibrios pueden ser estables o inestables, dependiendo de los valores de los parámetros.
- Dependencia de los Parámetros:
- El comportamiento del modelo es altamente dependiente de los valores de los parámetros. Cambios en la tasa de reproducción, eficiencia de caza, tasas de depredación y competencia pueden tener efectos significativos en las dinámicas del sistema.
En resumen, el modelo Lotka-Volterra proporciona una representación matemática de las interacciones cazador-presa en un ecosistema, y sus predicciones teóricas han sido la base para comprender las dinámicas de población en la ecología y la biología evolutiva.
Lotka-Volterra con Python
Puedes implementar el modelo Lotka-Volterra en Python utilizando el método de integración numérica. A continuación, te proporcionaré un ejemplo básico utilizando la biblioteca scipy para resolver las ecuaciones diferenciales y matplotlib para graficar las poblaciones de presa y depredador a lo largo del tiempo.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# Definir las ecuaciones diferenciales del modelo Lotka-Volterra
def lotka_volterra(t, y, alpha, beta, gamma, delta):
dxdt = alpha * y[0] - beta * y[0] * y[1]
dydt = delta * y[0] * y[1] - gamma * y[1]
return [dxdt, dydt]
# Parámetros del modelo
alpha = 0.1 # Tasa de crecimiento de presa en ausencia de depredador
beta = 0.02 # Eficiencia de caza de los depredadores
gamma = 0.1 # Tasa intrínseca de mortalidad de depredador
delta = 0.02 # Eficiencia de conversión de presas en nuevos depredadores
# Condiciones iniciales y tiempo de integración
initial_conditions = [40, 9] # Población inicial de presa y depredador
time_span = (0, 200) # Tiempo de integración de 0 a 200 unidades de tiempo
# Resolver las ecuaciones diferenciales
solution = solve_ivp(lotka_volterra, time_span, initial_conditions, args=(alpha, beta, gamma, delta), dense_output=True)
# Evaluar la solución en un conjunto de tiempo más fino para la visualización
t_fine = np.linspace(0, 200, 1000)
y_fine = solution.sol(t_fine)
# Graficar las poblaciones de presa y depredador a lo largo del tiempo
plt.figure(figsize=(10, 6))
plt.plot(t_fine, y_fine[0], label='Presa')
plt.plot(t_fine, y_fine[1], label='Depredador')
plt.title('Modelo Lotka-Volterra: Cazador-Presa')
plt.xlabel('Tiempo')
plt.ylabel('Población')
plt.legend()
plt.grid(True)
plt.show()En este código:
lotka_volterradefine las ecuaciones diferenciales del modelo Lotka-Volterra.solve_ivpse utiliza para resolver las ecuaciones diferenciales en el intervalo de tiempo especificado.- Se grafican las poblaciones de presa y depredador a lo largo del tiempo.
Este es un ejemplo básico, y puedes ajustar los parámetros y condiciones iniciales según tus necesidades específicas. Además, ten en cuenta que el modelo Lotka-Volterra es una simplificación y puede no capturar todas las complejidades de los ecosistemas en la naturaleza.
Otro ejemplo usando Python
El modelo Lotka-Volterra, que es comúnmente utilizado para describir las dinámicas de población entre depredadores y presas, puede analogarse a sistemas químicos en los que hay interacciones entre diferentes especies químicas. En lugar de poblaciones de animales, las variables representarán concentraciones de sustancias químicas. Aquí tienes un ejemplo sencillo de cómo podrías utilizar el modelo Lotka-Volterra en un contexto químico.
Supongamos que tenemos dos especies químicas A y B, y que participan en las siguientes reacciones químicas:
[ A \xrightarrow{k_1} 2A ]
[ 2A + B \xrightarrow{k_2} 3A ]
[ B \xrightarrow{k_3} \text{Productos} ]
Aquí, (k_1), (k_2), y (k_3) son constantes de velocidad para las respectivas reacciones. Podemos describir la dinámica de estas concentraciones utilizando el modelo Lotka-Volterra, aunque es importante señalar que esta es una analogía simplificada y que el modelo Lotka-Volterra en su forma clásica está más orientado hacia interacciones entre depredadores y presas.
Las ecuaciones diferenciales del modelo Lotka-Volterra para este sistema químico serían:
[ \frac{d[A]}{dt} = k_1 [A] – k_2 [A]^2[B] ]
[ \frac{d[B]}{dt} = -k_3 [B] + k_2 [A]^2[B] ]
Aquí, ([A]) y ([B]) representan las concentraciones de las especies químicas A y B, respectivamente.
Puedes utilizar estas ecuaciones junto con condiciones iniciales para ( [A] ) y ( [B] ) para simular la evolución de las concentraciones a lo largo del tiempo. Podrías implementar esto en Python utilizando la biblioteca scipy para resolver las ecuaciones diferenciales y matplotlib para graficar los resultados. A continuación, te presento un ejemplo básico:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Ecuaciones del modelo Lotka-Volterra para el sistema químico
def model(y, t, k1, k2, k3):
dAdt = k1 * y[0] - k2 * y[0]**2 * y[1]
dBdt = -k3 * y[1] + k2 * y[0]**2 * y[1]
return [dAdt, dBdt]
# Condiciones iniciales
A0 = 1.0
B0 = 2.0
y0 = [A0, B0]
# Parámetros del modelo
k1 = 0.1
k2 = 0.01
k3 = 0.05
# Tiempo de integración
t = np.linspace(0, 50, 100)
# Resolver las ecuaciones diferenciales
solution = odeint(model, y0, t, args=(k1, k2, k3))
# Graficar las concentraciones a lo largo del tiempo
plt.figure(figsize=(10, 6))
plt.plot(t, solution[:, 0], label='Concentración de A')
plt.plot(t, solution[:, 1], label='Concentración de B')
plt.xlabel('Tiempo')
plt.ylabel('Concentración')
plt.legend()
plt.grid(True)
plt.show()En este ejemplo, las concentraciones de A y B evolucionan con el tiempo según las ecuaciones del modelo Lotka-Volterra para el sistema químico especificado. Ajusta los parámetros y condiciones iniciales según tus necesidades específicas.
Transformada de Fourier
La Transformada de Fourier es una herramienta matemática fundamental en el análisis de señales y sistemas. Se utiliza para descomponer una señal en sus componentes de frecuencia, lo que permite analizar y manipular las características de la señal en el dominio de la frecuencia. La Transformada de Fourier se aplica en diversos campos, como procesamiento de señales, comunicaciones, imágenes, acústica, física, y muchas otras disciplinas.
Fundamento Matemático:
La Transformada de Fourier de una función ( f(t) ) en el tiempo (dominio temporal) se define como:
[ F(\omega) = \int_{-\infty}^{\infty} f(t) \cdot e^{-j\omega t} \,dt ]
donde:
- ( F(\omega) ) es la Transformada de Fourier de ( f(t) ) en el dominio de la frecuencia.
- ( \omega ) es la frecuencia angular (en radianes por segundo).
- ( j ) es la unidad imaginaria.
La Transformada de Fourier Inversa recupera la función en el dominio temporal a partir de su representación en el dominio de la frecuencia:
[ f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) \cdot e^{j\omega t} \,d\omega ]
Conceptos Clave:
- Dominio Temporal vs. Dominio de la Frecuencia:
- En el dominio temporal, representamos funciones en función del tiempo.
- En el dominio de la frecuencia, representamos funciones en función de las frecuencias presentes en la señal.
- Espectro de Frecuencia:
- La Transformada de Fourier proporciona el espectro de frecuencia de una señal, mostrando las contribuciones de cada frecuencia presente en la señal.
- Transformada de Fourier Discreta (DFT):
- En la práctica, las señales son discretas. La DFT es una versión discreta de la Transformada de Fourier que se aplica a secuencias discretas, como arreglos de datos.
- Transformada Rápida de Fourier (FFT):
- La FFT es un algoritmo eficiente para calcular la DFT, especialmente cuando se trabaja con señales digitales.
Usos y Aplicaciones:
- Análisis de Señales:
- Permite descomponer una señal en sus componentes frecuenciales, lo que facilita el análisis de su contenido espectral.
- Procesamiento de Imágenes y Sonido:
- En aplicaciones como compresión de imágenes y música, la Transformada de Fourier es esencial para analizar y manipular datos en el dominio de la frecuencia.
- Comunicaciones:
- Se utiliza en la modulación y demodulación de señales para transmitir información de manera eficiente a través de canales de comunicación.
- Física y Ciencia de Datos:
- En física, se aplica para analizar fenómenos periódicos. En ciencia de datos, se usa en análisis espectral y procesamiento de señales.
Cómo Usarla en Python:
En Python, la biblioteca numpy proporciona funciones para calcular la Transformada de Fourier y su inversa. Aquí hay un ejemplo simple:
import numpy as np
import matplotlib.pyplot as plt
# Crear una señal en el dominio temporal
t = np.linspace(0, 1, 1000, endpoint=False) # 1000 puntos en 1 segundo
signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.sin(2 * np.pi * 20 * t)
# Calcular la Transformada de Fourier
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(t), t[1] - t[0])
# Graficar la señal y su espectro de frecuencia
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('Señal en el Dominio Temporal')
plt.subplot(2, 1, 2)
plt.plot(frequencies, np.abs(fft_result))
plt.title('Espectro de Frecuencia')
plt.xlabel('Frecuencia (Hz)')
plt.tight_layout()
plt.show()Este es un ejemplo básico que crea una señal compuesta de dos componentes sinusoidales y luego calcula y grafica su Transformada de Fourier. Puedes experimentar con diferentes señales y ajustar los parámetros según tus necesidades.
Ejemplo Usando Python
La Transformada de Fourier (FT) se utiliza en química para analizar y entender propiedades espectroscópicas y fenómenos oscilatorios en diferentes sistemas químicos. Aquí te presento un ejemplo común de aplicación de la Transformada de Fourier en química, específicamente en espectroscopía de resonancia magnética nuclear (RMN), una técnica importante para el análisis estructural de compuestos químicos.
Ejemplo: Espectro de RMN y Transformada de Fourier
La RMN proporciona información sobre la estructura molecular y la conectividad atómica en una sustancia química. La señal de RMN es esencialmente un conjunto de funciones oscilatorias que representan las interacciones magnéticas de los núcleos atómicos con un campo magnético externo.
- Adquisición de Datos:
- Durante un experimento de RMN, se recopilan datos en el dominio del tiempo, que representan la señal de RMN en función del tiempo.
- Transformada de Fourier:
- Aplicar la Transformada de Fourier a los datos en el dominio del tiempo proporciona un espectro en el dominio de la frecuencia. [ S(f) = \int_{-\infty}^{\infty} s(t) \cdot e^{-j2\pi ft} \,dt ] Donde:
- ( S(f) ) es el espectro en el dominio de la frecuencia.
- ( s(t) ) es la señal en el dominio del tiempo.
- ( f ) es la frecuencia.
- Espectro de RMN en el Dominio de la Frecuencia:
- El espectro resultante en el dominio de la frecuencia proporciona información sobre las frecuencias de resonancia de los núcleos atómicos presentes en la muestra.
- Interpretación Estructural:
- Las frecuencias de resonancia se correlacionan con los entornos químicos y la conectividad atómica en la molécula. Las picos en el espectro de RMN en el dominio de la frecuencia se relacionan con los diferentes tipos de núcleos atómicos presentes.
Código en Python (Simulación Simplificada):
Vamos a realizar una simulación simple utilizando Python para ilustrar cómo se podría aplicar la Transformada de Fourier en un contexto de RMN. En este ejemplo, simularemos una señal de RMN compuesta por dos picos.
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# Parámetros de la simulación
sampling_rate = 1000 # Frecuencia de muestreo (Hz)
time_max = 1.0 # Duración de la señal en el dominio del tiempo (segundos)
frequency_peaks = [50, 200] # Frecuencias de los picos en Hz
# Generar señal de RMN simulada en el dominio del tiempo
t = np.linspace(0, time_max, int(sampling_rate * time_max), endpoint=False)
rmn_signal = np.sin(2 * np.pi * frequency_peaks[0] * t) + 0.5 * np.sin(2 * np.pi * frequency_peaks[1] * t)
# Aplicar la Transformada de Fourier
frequencies = fftfreq(len(t), 1/sampling_rate)
rmn_spectrum = fft(rmn_signal)
# Graficar la señal en el dominio del tiempo y su espectro en el dominio de la frecuencia
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, rmn_signal)
plt.title('Señal de RMN en el Dominio del Tiempo')
plt.xlabel('Tiempo (s)')
plt.subplot(2, 1, 2)
plt.plot(frequencies, np.abs(rmn_spectrum))
plt.title('Espectro de RMN en el Dominio de la Frecuencia')
plt.xlabel('Frecuencia (Hz)')
plt.tight_layout()
plt.show()Este código simula una señal de RMN en el dominio del tiempo y luego aplica la Transformada de Fourier para obtener el espectro en el dominio de la frecuencia. En una aplicación práctica, la señal de RMN provendría de datos experimentales obtenidos en un espectrómetro de RMN real.