Ajuste de Funciones a Datos Experimentales: Un Enfoque Holístico para la Interpretación Científica
El ajuste de funciones a datos experimentales es una herramienta fundamental en la investigación científica. Permite modelar y entender las relaciones subyacentes entre variables, facilitando la extrapolación, la predicción y la identificación de patrones en los datos.
¿Qué es el Ajuste de Funciones?
El ajuste de funciones implica encontrar una expresión matemática que describa de manera óptima la relación entre las variables medidas en un experimento. Es esencial para transformar datos experimentales en modelos cuantitativos que puedan interpretarse y utilizarse para hacer predicciones. Aquí, desglosaremos los conceptos clave:
Ajuste Lineal:

El ajuste lineal busca encontrar la mejor línea recta que se ajuste a un conjunto de datos. La ecuación general de una línea es (y = mx + b), donde (m) es la pendiente y (b) es la ordenada al origen. Para encontrar la mejor línea, se utilizan métodos como el método de mínimos cuadrados, que minimiza la suma de los cuadrados de las diferencias entre los valores reales y los predichos por la línea.
Ajuste No Lineal:
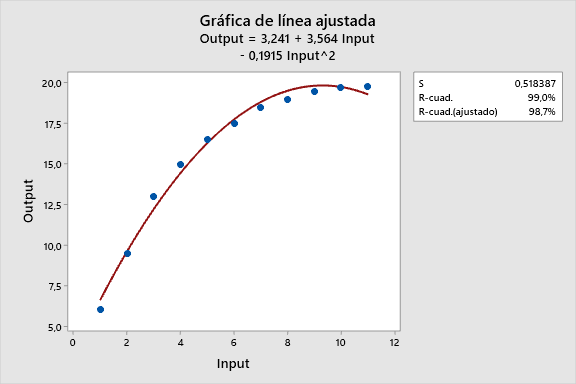
Cuando la relación entre las variables no puede modelarse eficientemente con una línea recta, se emplea un ajuste no lineal. Este método implica encontrar una función más compleja que se ajuste mejor a los datos. Pueden usarse funciones exponenciales, polinomios de grado superior, logaritmos, entre otras. El proceso de ajuste implica ajustar los parámetros de la función para minimizar la diferencia entre los datos reales y los estimados por la función.
Términos Claves:
- Ajuste a una Curva: Este término se refiere al proceso global de encontrar la función que mejor se adapte a un conjunto de datos, ya sea lineal o no lineal.
- Mejor Ajuste: El mejor ajuste es el resultado óptimo del proceso de ajuste, minimizando las discrepancias entre los datos experimentales y los valores predichos por la función ajustada.
- Coeficientes de Ajuste: Son los parámetros de la función ajustada que se optimizan durante el proceso para lograr el mejor ajuste.
- Errores Residuales: La diferencia entre los valores medidos y los predichos. La minimización de estos errores es esencial para obtener un ajuste robusto.
- R-cuadrado (R²): Una medida de cuánto la variabilidad en los datos es explicada por el modelo ajustado. Un valor cercano a 1 indica un buen ajuste.
- Método de Mínimos Cuadrados: Una técnica matemática que minimiza la suma de los cuadrados de las diferencias entre los valores observados y los predichos.
Ejemplo Práctico
Ejemplo
Ejemplo Práctico:
Supongamos un conjunto de datos de decaimiento exponencial:
| Tiempo (s) | Concentración (mol/L) |
|------------|------------------------|
| 0 | 1.0 |
| 10 | 0.9 |
| 20 | 0.8 |
| 30 | 0.7 |
| 40 | 0.6 |Ajuste Lineal:
import numpy as np
import matplotlib.pyplot as plt
# Implementación en Python del ajuste lineal
tiempo = np.array([0, 10, 20, 30, 40])
concentracion = np.array([1.0, 0.9, 0.8, 0.7, 0.6])
# Ajuste lineal
coeficientes = np.polyfit(tiempo, concentracion, 1)
linea_ajustada = np.polyval(coeficientes, tiempo)
# Visualización de los resultados
plt.scatter(tiempo, concentracion, label='Datos Experimentales')
plt.plot(tiempo, linea_ajustada, label='Ajuste Lineal', color='red')
plt.xlabel('Tiempo (s)')
plt.ylabel('Concentración (mol/L)')
plt.legend()
plt.show()Este código utiliza el método de mínimos cuadrados para encontrar la línea que mejor se ajusta a los datos de decaimiento exponencial.
Análisis de Regresión
Análisis de Regresión: Un Pilar Fundamental en la Exploración Científica
El análisis de regresión se presenta como un método poderoso en el arsenal de herramientas científicas, especialmente en disciplinas como química, quimiometría, fisicoquímica, física y matemáticas. Este análisis se destaca por su versatilidad en la modelización y predicción de fenómenos, así como su importancia en la toma de decisiones fundamentadas. A continuación, se detallan sus conceptos esenciales y su relevancia en la exploración y comprensión de datos.
¿Qué es el Análisis de Regresión?
El análisis de regresión es una técnica estadística utilizada para investigar y modelar la relación entre una variable dependiente y una o más variables independientes. En esencia, busca entender cómo los cambios en las variables independientes afectan a la variable dependiente. Se basa en la construcción de un modelo matemático que describe y cuantifica esta relación.
¿Para qué Sirve?
- Modelización Cuantitativa:
- Permite expresar de manera cuantitativa la relación entre variables, facilitando la interpretación precisa de fenómenos complejos.
- Predicción y Extrapolación:
- Facilita la predicción de valores futuros basados en patrones observados, proporcionando una herramienta valiosa para la planificación y toma de decisiones.
- Identificación de Tendencias:
- Ayuda a identificar patrones y tendencias en los datos, permitiendo una comprensión más profunda del comportamiento de las variables en estudio.
Importancia de Obtener Parámetros de Regresión:
La obtención de los parámetros de regresión, como las pendientes y las intersecciones, es crucial en el proceso. Estos parámetros definen la ecuación del modelo y determinan la forma en que las variables independientes influyen en la variable dependiente. La precisión en la estimación de estos parámetros asegura que el modelo sea representativo y útil para describir la relación subyacente en los datos.
Estimación de la Bondad de Ajuste:
La bondad de ajuste, evaluada mediante estadísticas como el coeficiente de determinación ((R^2)), es esencial para medir cuán bien el modelo se ajusta a los datos experimentales. Un (R^2) cercano a 1 indica un ajuste sólido, mientras que valores más bajos sugieren que el modelo no explica de manera efectiva la variabilidad en los datos. Evaluar la bondad de ajuste es crucial para determinar la validez y confiabilidad del modelo.
Conclusión:
En resumen, el análisis de regresión se erige como un pilar fundamental en la exploración y comprensión de fenómenos científicos. La obtención precisa de parámetros de regresión y la evaluación de la bondad de ajuste garantizan que los modelos desarrollados sean representativos y confiables.
Regresión Lineal
Regresión Lineal: Desentrañando Relaciones Lineales con Precisión
La regresión lineal es una técnica fundamental en el análisis de datos, especialmente en contextos científicos y matemáticos. Se utiliza para modelar y entender la relación entre una variable dependiente y una o más variables independientes. Profundicemos en la regresión lineal y los métodos asociados para su aplicación:
¿Qué es la Regresión Lineal?
La regresión lineal es un método estadístico que busca encontrar la mejor línea recta que se ajusta a un conjunto de datos. La ecuación general de una línea recta es de la forma (y = mx + b), donde (y) es la variable dependiente, (x) es la variable independiente, (m) es la pendiente y (b) es la ordenada al origen. El objetivo es determinar los valores de (m) y (b) que minimizan la suma de los cuadrados de las diferencias entre los valores observados y los predichos por la línea.
Métodos para Aplicar la Regresión Lineal:
- Método de Mínimos Cuadrados: Este es el método más comúnmente utilizado en la regresión lineal. Busca minimizar la suma de los cuadrados de las diferencias entre los valores reales y los predichos por la línea. Los parámetros (m) y (b) se calculan analíticamente.
- Método de Gradiente Descendente: Este método es iterativo y se basa en ajustar los parámetros de la línea gradualmente en la dirección que minimiza el error. Es especialmente útil cuando se trabaja con conjuntos de datos grandes.
Pasos para Aplicar la Regresión Lineal:
- Recopilación de Datos: Recolectar datos de las variables de interés.
- Exploración y Visualización: Explorar y visualizar los datos para identificar posibles relaciones lineales.
- Definición del Modelo: Elegir el modelo de regresión lineal y la forma de la ecuación.
- Estimación de Parámetros: Utilizar métodos como el de mínimos cuadrados para estimar los parámetros de la línea.
- Validación del Modelo: Evaluar la bondad de ajuste mediante estadísticas como el coeficiente de determinación ((R^2)).
- Predicciones y Análisis: Utilizar el modelo para realizar predicciones y analizar la relación entre las variables.
Importancia de la Regresión Lineal:
- Simplicidad Interpretativa: La linealidad facilita la interpretación del efecto de las variables independientes sobre la variable dependiente.
- Implementación Generalizada: A pesar de su simplicidad, la regresión lineal se aplica de manera efectiva en una amplia gama de problemas y disciplinas.
- Base para Métodos Avanzados: Sirve como base para métodos más complejos y avanzados en estadística y aprendizaje automático.
En la aplicación de la regresión lineal, es esencial entender el contexto del problema y elegir el método más adecuado para los datos disponibles. Con tu experticia en programación en Python y métodos numéricos, puedes implementar eficientemente estos métodos para obtener modelos precisos y significativos.
Mínimo Cuadrados
Regresión por Mínimos Cuadrados: Fundamentos Analíticos para la Precisión
La regresión por mínimos cuadrados es una técnica estadística crucial que busca encontrar la línea que mejor se ajusta a un conjunto de datos. Su objetivo es minimizar la suma de los cuadrados de las diferencias entre los valores observados y los predichos por la línea de regresión. Aquí están los fundamentos analíticos y las ecuaciones necesarias para llevar a cabo este tipo de regresión:
Ecuaciones para la Regresión Lineal por Mínimos Cuadrados:
Supongamos que tenemos (n) pares de observaciones ((x_i, y_i)), donde (x_i) es la variable independiente y (y_i) es la variable dependiente.
Ecuación de la Línea de Regresión: La ecuación de la línea de regresión lineal simple es:
\[[y=mx+b]\]
donde (m) es la pendiente y (b) es la ordenada al origen.
Cálculo de la Pendiente ((m)): La fórmula para la pendiente ((m)) es:
\[[m=\frac{n(\sum_{ }^{ }xy)-(\sum_{ }^{ }x)(\sum_{ }^{ }y)}{n(\sum_{ }^{ }x^2)-(\sum_{ }^{ }x)^2}]\]
\[(\sum_{ }^{ })\ representa\ la\ Suma,\ n\ es\ el\ número\ de\ observaciones.\]
x la variable independiente, y la variable dependiente y xy es el producto de x con y
Cálculo de la Ordenada al Origen ((b)): La fórmula para la ordenada al origen ((b)) es:
\[[b=\frac{(\sum_{ }^{ }y)-m(\sum_{ }^{ }x)}{n}]\]
Ecuación de Regresión Lineal Completa: Una vez que se han calculado (m) y (b), la ecuación de regresión lineal completa es:
[ y = \frac{n(\sum xy) - (\sum x)(\sum y)}{n(\sum x^2) - (\sum x)^2} \cdot x + \frac{(\sum y) - m(\sum x)}{n} ]Proceso Resumido:
Calcule las Sumas:
( \sum x, \sum y, \sum xy, \sum x^2 )
Aplique las Fórmulas: Utilice las fórmulas para calcular (m) y (b).
Construya la Ecuación de Regresión: Combine (m), (b), (x), y (y) para formar la ecuación de regresión.
Interpretación de los Coeficientes:
- Pendiente ((m)): Representa el cambio promedio en (y) por cada unidad de cambio en (x).
- Ordenada al Origen ((b)): Indica el valor estimado de (y) cuando (x) es cero.
La regresión por mínimos cuadrados es una herramienta poderosa para ajustar modelos lineales a datos. Con tus habilidades en programación en Python, puedes automatizar estos cálculos y realizar regresiones eficientes, proporcionando una comprensión más profunda de las relaciones entre las variables.
Mínimo Cuadrados con Python
Para realizar una regresión por mínimos cuadrados en Python, podemos utilizar bibliotecas como NumPy y matplotlib. Vamos a crear un ejemplo sencillo con datos de muestra:
import numpy as np
import matplotlib.pyplot as plt
# Datos de muestra
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 4, 5])
# Cálculo de la pendiente (m) y la ordenada al origen (b)
n = len(x)
m = (n * np.sum(x * y) - np.sum(x) * np.sum(y)) / (n * np.sum(x**2) - (np.sum(x))**2)
b = (np.sum(y) - m * np.sum(x)) / n
# Ecuación de regresión lineal
regression_line = m * x + b
# Visualización de los resultados
plt.scatter(x, y, label='Datos de muestra')
plt.plot(x, regression_line, color='red', label='Regresión lineal')
plt.xlabel('Variable Independiente (x)')
plt.ylabel('Variable Dependiente (y)')
plt.title('Regresión por Mínimos Cuadrados')
plt.legend()
plt.show()
# Imprimir la ecuación de regresión
print(f"Ecuación de regresión: y = {m:.2f}x + {b:.2f}")En este ejemplo, hemos creado dos arrays NumPy, x e y, que representan nuestras variables independiente y dependiente, respectivamente. Luego, hemos utilizado las fórmulas de la regresión por mínimos cuadrados para calcular la pendiente (m) y la ordenada al origen (b). Finalmente, hemos visualizado los datos de muestra junto con la línea de regresión resultante.
Este código es un punto de partida básico, y en aplicaciones del mundo real, podrías trabajar con conjuntos de datos más grandes y complejos. Además, bibliotecas más avanzadas como scikit-learn también ofrecen herramientas robustas para realizar regresiones en Python.
Mínimo Cuadrados con Excel
Como profesor con experiencia en enseñanza de química, quimiometría, fisicoquímica, física, matemáticas y programación en Python, puedo guiarte en la implementación de una regresión por mínimos cuadrados en Excel. Aquí te dejo un paso a paso utilizando las funciones incorporadas en Excel:
Supongamos que tienes tus datos organizados en dos columnas, con la variable independiente (x) en la columna A y la variable dependiente (y) en la columna B.
Pasos para Implementar la Regresión por Mínimos Cuadrados en Excel:
- Organiza tus Datos: Asegúrate de tener tus datos organizados en columnas adyacentes.
- Inserta el Gráfico de Dispersión: Selecciona tus datos.
Ve a la pestaña “Insertar” y selecciona “Gráfico de dispersión”. - Añade una Línea de Regresión: Haz clic derecho en uno de los puntos en el gráfico.
Selecciona “Agregar línea de tendencia”. - Elige el Tipo de Regresión: En el cuadro de diálogo que aparece, elige “Lineal” u otro tipo de regresión según tus necesidades.
- Muestra la Ecuación y el Coeficiente de Determinación en el Gráfico: Marca las opciones “Mostrar ecuación en el gráfico” y “Mostrar valor R cuadrado en el gráfico”.
- Obtén los Parámetros de Regresión: Excel calculará automáticamente los parámetros de la regresión (pendiente, ordenada al origen, etc.) y mostrará la ecuación y el (R^2) en el gráfico.
Uso de Funciones en Excel:
- Ecuación de Regresión (Pendiente y Ordenada al Origen):
- Para obtener la pendiente ((m)) y la ordenada al origen ((b)), puedes usar las funciones
PENDIENTEeINTERSECCIÓN.
=PENDIENTE(B2:B10, A2:A10)
=INTERSECCIÓN(B2:B10, A2:A10)Donde B2:B10 son tus datos de la variable dependiente y A2:A10 son tus datos de la variable independiente.
- Coeficiente de Determinación ((R^2)):
- Excel calcula automáticamente (R^2) cuando añades una línea de tendencia. Si deseas obtenerlo por separado, puedes usar la función
R2.
=R2(B2:B10, PREDICCION.LINEAL(A2:A10, B2:B10, A2:A10))Donde B2:B10 son tus datos reales y PREDICCION.LINEAL es la función que predice los valores utilizando la regresión lineal.
Siguiendo estos pasos, podrás implementar una regresión por mínimos cuadrados en Excel y obtener los parámetros de la regresión junto con el (R^2). Esto proporcionará una representación visual y cuantitativa de la relación entre tus variables.
El Gradiente Descendente
El gradiente descendente es una técnica de optimización fundamental en el campo de la machine learning y la optimización numérica.
Gradiente Descendente: Conceptos Básicos:
El gradiente descendente es un algoritmo de optimización utilizado para encontrar el mínimo local de una función. Su aplicación es clave en:
- Aprendizaje Automático (Machine Learning): Se utiliza para minimizar la función de costo, ajustando los parámetros de un modelo para hacer predicciones más precisas.
- Optimización Numérica: Puede aplicarse en problemas más generales para encontrar mínimos o máximos de funciones.
Principio Básico:
El concepto central del gradiente descendente es la derivada de la función objetivo en el punto actual. La derivada indica la dirección en la cual la función está creciendo más rápidamente. El gradiente descendente da pasos proporcionales a la negativa de la derivada, moviéndose hacia el mínimo local.
Pasos Básicos para Implementar el Gradiente Descendente:
- Inicialización: Selecciona un punto de inicio en el espacio de parámetros.
- Cálculo del Gradiente: Calcula la derivada de la función objetivo en el punto actual.
- Actualización de Parámetros: Ajusta los parámetros en dirección opuesta al gradiente, multiplicado por una tasa de aprendizaje.
- Iteración: Repite los pasos 2 y 3 hasta que se alcance un criterio de convergencia (por ejemplo, número máximo de iteraciones o cambio mínimo en la función objetivo).
Python y Gradiente Descendente:
En Python, el gradiente descendente puede implementarse eficientemente. Supongamos que tienes una función objetivo (J(\theta)) que deseas minimizar en términos de un vector de parámetros (\theta).
def gradient_descent(theta, learning_rate, num_iterations):
for _ in range(num_iterations):
gradient = compute_gradient(theta) # Calcular el gradiente
theta = theta - learning_rate * gradient # Actualizar los parámetros
return thetaConsideraciones:
- Tasa de Aprendizaje (Learning Rate): La elección adecuada de la tasa de aprendizaje es crucial. Una tasa demasiado pequeña puede llevar a convergencia lenta, mientras que una tasa demasiado grande puede hacer que el algoritmo diverja.
- Inicialización de Parámetros: La elección inicial de los parámetros también es importante. Puede afectar la convergencia y la calidad de la solución.
Aplicación en Machine Learning:
En aprendizaje automático, el gradiente descendente se aplica para ajustar los pesos y sesgos de un modelo, minimizando la función de costo. Lo que hace que la red neuronal pueda mejorar con cada nuevo ciclo de prueba.
Enseñanza Práctica:
Podrías realizar ejercicios prácticos implementando el gradiente descendente en Python, quizás optimizando parámetros en un modelo simple.
En resumen, el gradiente descendente es una herramienta esencial en optimización numérica y aprendizaje automático, y su comprensión y aplicación son valiosas para explorar y resolver problemas en diversos campos.
Algunos usos de la Regresión Lineal en Química
La regresión lineal se utiliza comúnmente en química para analizar relaciones entre variables y hacer predicciones. A continuación verás algunos ejemplos del uso de la regresión lineal en química.
- Cinética Química: En el estudio de la velocidad de reacciones químicas, la regresión lineal se puede utilizar para determinar la constante de velocidad. La relación lineal entre la concentración de reactantes y el tiempo de reacción es fundamental en la cinética química.
- Calibración de Instrumentos: En análisis instrumental, como la espectroscopia o la cromatografía, se utiliza la regresión lineal para calibrar instrumentos y correlacionar la señal medida con la concentración de una sustancia química.
- Estequiometría: La regresión lineal puede aplicarse en problemas estequiométricos para determinar la relación cuantitativa entre las cantidades de reactivos y productos en una reacción química.
- Termodinámica: En experimentos termodinámicos, como la determinación de entalpías de reacción, la regresión lineal se utiliza para ajustar datos experimentales y calcular parámetros termodinámicos.
- Análisis de Datos Experimentales: En general, la regresión lineal se aplica en la interpretación de datos experimentales, como en la construcción de curvas de calibración, ajuste de modelos a datos espectroscópicos, o determinación de constantes de equilibrio.
- Estudio de Equilibrios Ácido-Base: En química analítica, la regresión lineal puede usarse para estudiar equilibrios ácido-base al medir el pH en función de la concentración de ácido o base.
- Determinación de Constantes de Equilibrio: La regresión lineal se emplea para determinar constantes de equilibrio en reacciones químicas, como en el caso de equilibrios heterogéneos o la solubilidad de compuestos.
- Análisis de Concentraciones: En análisis químico cuantitativo, la regresión lineal se utiliza para relacionar la concentración de una sustancia con la absorbancia medida en técnicas como la espectrofotometría.
- Correlación de Propiedades Físico-Químicas: La regresión lineal se aplica para correlacionar propiedades físico-químicas, como la relación entre la temperatura y la solubilidad de un compuesto.
Estos ejemplos demuestran la versatilidad de la regresión lineal en química, desde el estudio de la cinética y la termodinámica hasta la calibración de instrumentos y la interpretación de datos experimentales.
Regresión Lineal Múltiple
Regresión Lineal Múltiple: Conceptos Básicos
La regresión lineal múltiple es una técnica estadística utilizada para modelar la relación entre una variable dependiente y dos o más variables independientes. A diferencia de la regresión lineal simple, que considera solo una variable independiente, la regresión lineal múltiple maneja múltiples variables predictoras.
Fundamento Matemático:
La ecuación general de la regresión lineal múltiple se expresa como:
[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n + \epsilon ]
- ( Y ) es la variable dependiente.
- ( \beta_0 ) es la ordenada al origen.
- ( \beta_1, \beta_2, \ldots, \beta_n ) son los coeficientes que representan la relación entre cada variable independiente (X_i) y la variable dependiente.
- ( X_1, X_2, \ldots, X_n ) son las variables independientes.
- ( \epsilon ) es el término de error.
El objetivo es encontrar los coeficientes ( \beta_0, \beta_1, \ldots, \beta_n ) que minimizan la suma de los cuadrados de los residuos, utilizando un método como el de mínimos cuadrados.
Cómo Utilizar la Regresión Lineal Múltiple:
- Recopilación de Datos: Recopila datos que incluyan una variable dependiente y dos o más variables independientes.
- Ajuste del Modelo: Utiliza técnicas estadísticas o herramientas como el método de mínimos cuadrados para ajustar el modelo a los datos.
- Validación del Modelo: Evalúa la validez del modelo mediante pruebas estadísticas y técnicas de validación cruzada.
- Interpretación de Coeficientes: Examina los coeficientes para entender la contribución relativa de cada variable independiente a la variable dependiente.
Cuándo Usar la Regresión Lineal Múltiple:
La regresión lineal múltiple es apropiada cuando se sospecha que varias variables independientes están relacionadas con la variable dependiente y se desea entender cómo estas variables influyen conjuntamente. Algunas situaciones comunes incluyen:
- Modelado Predictivo: Cuando se busca predecir una variable dependiente utilizando múltiples variables predictoras.
- Control de Variables Confusas: Cuando se desea controlar o ajustar los efectos de variables adicionales que podrían influir en la variable dependiente.
- Análisis de Datos Multidimensionales: Cuando se trabaja con conjuntos de datos que incluyen múltiples variables de entrada.
Por Qué Utilizar la Regresión Lineal Múltiple:
- Captura Relaciones Complejas: Permite modelar relaciones más complejas que la regresión lineal simple al considerar múltiples variables independientes.
- Control de Variables: Ofrece la capacidad de controlar o ajustar los efectos de variables adicionales que podrían afectar la relación entre las variables de interés.
- Mayor Precisión en Predicciones: Al incorporar múltiples variables predictoras, la regresión lineal múltiple puede proporcionar predicciones más precisas y robustas.
- Análisis de Contribuciones Individuales: Permite evaluar las contribuciones relativas de cada variable independiente en el modelo.
En resumen, la regresión lineal múltiple es una herramienta valiosa cuando se desea entender y modelar relaciones más complejas entre variables. Se aplica en una variedad de disciplinas, desde ciencias sociales hasta ciencias físicas y biológicas, para hacer predicciones y analizar la influencia conjunta de múltiples factores.
Implementando la Regresión Lineal Múltiple con Excel y Python
Regresión Lineal Múltiple con Excel:
Realizar una regresión lineal múltiple en Excel es posible utilizando la función de análisis de datos. Aquí hay un paso a paso detallado:
- Preparación de Datos: Organiza tus datos en una hoja de cálculo de Excel. Asegúrate de tener una columna para la variable dependiente y columnas separadas para cada variable independiente.
- Habilitar el Complemento “Analysis ToolPak”:
Ve a la pestaña “Archivo” -> “Opciones” -> “Complementos”.
Selecciona “Complementos de Excel” en el cuadro “Administrar” y haz clic en “Ir”.
Marca “Analysis ToolPak” y haz clic en “Aceptar”. - Cargar Datos y Seleccionar Herramienta de Análisis: Ve a la pestaña “Datos” y selecciona “Análisis de datos” en el grupo “Herramientas de datos”.
- Elegir Regresión: En el cuadro de diálogo “Análisis de datos”, elige “Regresión” y haz clic en “Aceptar”.
- Configurar la Regresión: En la ventana de configuración, especifica la columna de la variable dependiente, las columnas de las variables independientes y el rango de salida. Puedes elegir si deseas que se muestren estadísticas adicionales.
Haz clic en “Aceptar” y Excel calculará los coeficientes de la regresión y otras estadísticas. - Interpretar Resultados:Examinar los resultados generados, especialmente los coeficientes de regresión y las estadísticas de ajuste del modelo.
Regresión Lineal Múltiple con Python:
En Python, puedes utilizar la biblioteca scikit-learn para realizar una regresión lineal múltiple. Aquí hay un ejemplo detallado:
# Importar bibliotecas necesarias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
# Crear un DataFrame con los datos
# Supongamos que tienes un archivo CSV llamado 'datos.csv'
datos = pd.read_csv('datos.csv')
# Definir variables independientes (X) y dependiente (Y)
X = datos[['Variable1', 'Variable2', 'Variable3']]
Y = datos['VariableDependiente']
# Dividir los datos en conjuntos de entrenamiento y prueba
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# Crear el modelo de regresión lineal múltiple
modelo = LinearRegression()
# Ajustar el modelo a los datos de entrenamiento
modelo.fit(X_train, Y_train)
# Realizar predicciones en el conjunto de prueba
predicciones = modelo.predict(X_test)
# Evaluar el rendimiento del modelo
print('Coeficientes:', modelo.coef_)
print('Intercepto:', modelo.intercept_)
print('Error Cuadrático Medio:', metrics.mean_squared_error(Y_test, predicciones))Este script de Python asume que tienes un conjunto de datos en formato CSV llamado ‘datos.csv’. Ajusta los nombres de las variables y el archivo según tu situación.
Al ejecutar este script, obtendrás información sobre los coeficientes de regresión, el intercepto y el error cuadrático medio del modelo. Este es solo un ejemplo básico; puedes personalizarlo según tus necesidades específicas.
Regresión No Lineal
Regresión No Lineal: Conceptos Básicos
La regresión no lineal es un enfoque estadístico que modela la relación entre una variable dependiente y una o más variables independientes de manera no lineal. A diferencia de la regresión lineal, en la regresión no lineal, la relación entre las variables no se describe mediante una ecuación lineal.
Fundamentos Matemáticos:
La forma general de una regresión no lineal puede expresarse como:
[ Y = f(X, \beta) + \epsilon ]
- ( Y ) es la variable dependiente.
- ( X ) son las variables independientes.
- ( \beta ) son los parámetros del modelo que se deben estimar.
- ( f(X, \beta) ) es una función no lineal de ( X ) y ( \beta ).
- ( \epsilon ) es el término de error.
En lugar de ajustar una línea recta, como en la regresión lineal, la regresión no lineal ajusta una curva que mejor se ajusta a los datos.
Cuándo Utilizar la Regresión No Lineal:
Se utiliza la regresión no lineal cuando se sospecha o se ha demostrado que la relación entre las variables no puede modelarse de manera efectiva con una ecuación lineal. Algunas situaciones comunes incluyen:
- Comportamiento Exponencial o Logarítmico: Cuando los datos sugieren un crecimiento o decrecimiento exponencial o logarítmico.
- Modelado de Fenómenos Naturales: Para modelar fenómenos naturales donde las leyes físicas o biológicas indican una relación no lineal.
- Ajuste de Curvas Específicas: Cuando se desea ajustar datos a una forma específica de curva (polinómica, exponencial, logarítmica, etc.).
- Modelado de Procesos Físicos o Químicos: En ciencias físicas o químicas, donde las relaciones pueden seguir leyes específicas que no son lineales.
Cómo Utilizar la Regresión No Lineal:
- Selección de Modelo: Identifica el tipo de función no lineal que mejor describe la relación entre las variables. Puedes necesitar conocimiento previo o realizar análisis exploratorios.
- Estimación de Parámetros: Utiliza métodos numéricos para estimar los parámetros del modelo que mejor ajustan los datos.
- Validación del Modelo: Evalúa la validez del modelo utilizando métricas estadísticas y gráficos de residuos.
Por Qué Utilizar la Regresión No Lineal:
- Mayor Flexibilidad: Permite modelar una variedad más amplia de relaciones entre variables que la regresión lineal.
- Ajuste a Fenómenos Complejos: Útil para fenómenos que no siguen una relación simple y lineal.
- Mejora de la Precisión: Puede mejorar la precisión del ajuste al tener en cuenta patrones no lineales en los datos.
Métodos para Aplicar la Regresión No Lineal:
- Mínimos Cuadrados No Lineales: Este método minimiza la suma de los cuadrados de las diferencias entre los valores observados y los valores predichos por el modelo.
- Método de Newton-Raphson: Un método iterativo que se utiliza para encontrar raíces de ecuaciones, también se puede aplicar para estimar parámetros en regresiones no lineales.
- Método de Levenberg-Marquardt: Un algoritmo de optimización iterativo que combina las ventajas de los métodos de gradiente descendente y Newton-Raphson.
- Método de Gauss-Newton: Similar al método de Newton-Raphson pero diseñado específicamente para problemas de mínimos cuadrados no lineales.
- Regresión No Lineal por Segmentos: Divide los datos en segmentos y ajusta un modelo no lineal a cada segmento, permitiendo un ajuste más flexible.
Ejemplo de Regresión No Lineal con Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# Datos de ejemplo
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.3, 4.5, 7.2, 9.8, 12.5])
# Función exponencial como modelo
def modelo_exponencial(x, a, b):
return a * np.exp(b * x)
# Ajuste de la curva utilizando curve_fit
parametros, covarianza = curve_fit(modelo_exponencial, x, y)
# Predicciones con los parámetros ajustados
y_pred = modelo_exponencial(x, *parametros)
# Gráfica de los datos y la curva ajustada
plt.scatter(x, y, label='Datos')
plt.plot(x, y_pred, label='Ajuste Exponencial', color='red')
plt.legend()
plt.show()Este ejemplo utiliza la biblioteca scipy para ajustar una función exponencial a datos de ejemplo. Ajustar otros tipos de funciones sigue un enfoque similar utilizando métodos específicos para regresión no lineal.